力矩是矢量而不是代數量,定義是位移和力矢量的矢積。
力矩的方向,是用矢量運算法則確定的,即右手四指的彎曲方向從位移方向沿著小于180度的夾角方向轉向力矢量時大拇指的指向,如果這個方向和假定的正方向相同就記為正,否則記為負。
實際當中這樣做比較麻煩,我們可以從假定的正方向看過去,如果這個力使物體產生逆時針方向的轉動,我們就記這個力的力矩為正,否則就記為負。
力是對點的平移作用,當然經由該點可以帶動線面體,力矩是實際兩個力組成的(參照系),力矩是對直線的旋轉作用。假設都是1牛頓的力,作用于一點,你如何區分他們?答案就是方向,這無數哥方向在3維世界中形成球,類似的,假設都是1牛米的力矩,作用于一條直線,你如何區分他們?答案也是方向,不同的力矩作用,旋轉方向是不一樣的,每個旋轉方向都確定了一個平面,對于直線來說,你在其上任意一點安插一條法線,那它的旋轉也就唯一了,也就是說法線能區分不同方向的力矩,所以旋轉平面的法線就是力矩的方向,至于順時針逆時針,就像力向前向后一樣,是相反的,所以是正負的關系。
力矩的量綱是距離×力;與能量的量綱相同。但是力矩通常用牛頓-米,而不是用焦耳作為單位。力矩的單位由力和力臂的單位決定。
力對物體產生轉動作用的物理量。可分為力對軸的矩和力對點的矩。力對軸的矩是力對物體產生繞某一軸轉動作用的物理量。它是代數量,其大小等于力在垂直于該軸的平面上的分力同此分力作用線到該軸垂直距離的乘積;其正負號用以區別力矩的不同轉向,按右手螺旋定則確定:以右手四指沿分力方向(X軸/Y軸),且掌心面向轉軸(X軸/Y軸)而握拳,大拇指方向(Z軸)與該軸正向一致時取正號,反之則取負號。力對點的矩是力對物體產生繞某一點轉動作用的物理量。它是矢量,等于力作用點位置矢r和力矢F的矢量積。例如 ,用球鉸鏈固定于O點的物體受力F作用,以r表示自O點至F作用點A的位置矢,r和F的夾角為a(見圖)。物體在F作用下 ,繞垂直于r與F組成的平面并通過O點的軸轉動 。轉動作用的大小和轉軸的方向取決于F對O點的矩矢M,M=r×F ;M的大小為rFsina ,方向由右手定則確定 。力矩M 在過矩心O的直角坐標軸上的投影為 Mx 、My 、Mz 。可以證明 Mx 、My 、Mz 就是F對x ,y,z軸的矩。力矩的量綱為L2MT -2,其國際制單位為N·m。
右手定則判斷力矩的方向
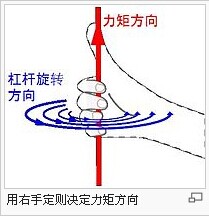
力矩等于作用于杠桿的作用力乘以支點到力的垂直距離。例如,3 牛頓的作用力,施加于離支點2 米處,所產生的力矩,等于1牛頓的作用力,施加于離支點6米處,所產生的力矩。力矩是個矢量。力矩的方向與它所造成的旋轉運動的旋轉軸同方向。力矩的方向可以用右手定則來決定。假設作用力垂直于杠桿。將右手往杠桿的旋轉方向彎卷,伸直的大拇指與支點的旋轉軸同直線,則大拇指指向力矩的方向。
